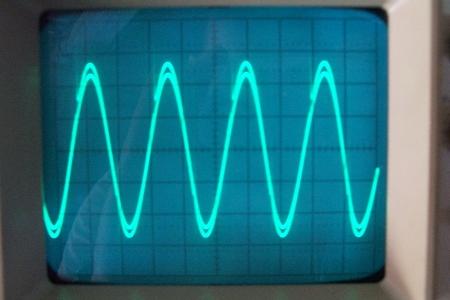
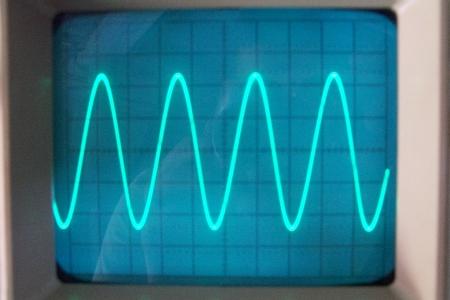
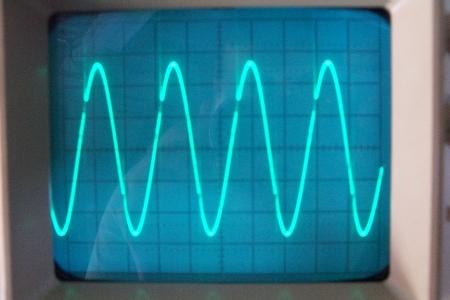
Expérience échouée – MEG : une machine à énergie libre qui ne marche pas
Générateur Électromagnétique sans Mouvement
(Motionless Electromagnetic Generator)
Même si cette invention ne marche pas après tests, je diffuse les comptes-rendus d’expérience pas à pas pour vous donner une idée de l’énergie et du temps à déployer pour tester UNE invention. En 1990 sur 10 inventions données 9 environ étaient des faux mais 1 sur 10 présentait une vraie anomalie de surunité (énergie libre). Puis 10 ans après on est passé à 99 faux sur 100 et de nous jours en 2015 on est plutôt à 999 faux sur 1000. C’est la stratégie des lobbys énergétiques: susciter la diffusion d’un maximum de faux pour que les quelques uns qui marchent soient noyés dans la masse, quand on voit le temps, argent, et énergie nécessaires pour tester une invention donnée on comprend comment sont découragés les expérimentateurs ainsi.
Qu’est-ce que c’est ?
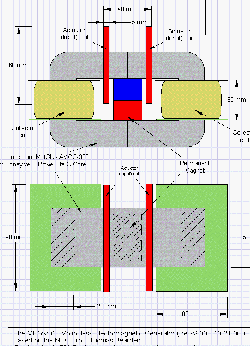
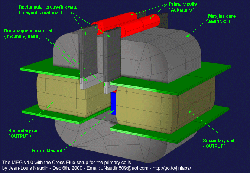
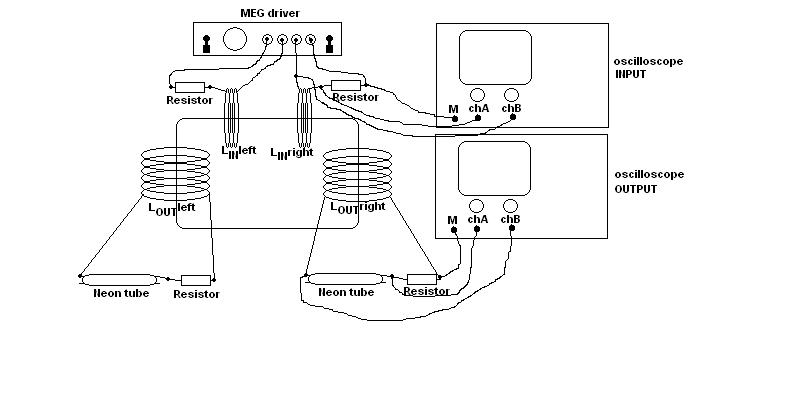
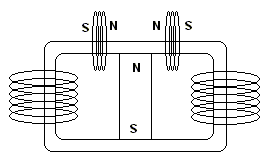
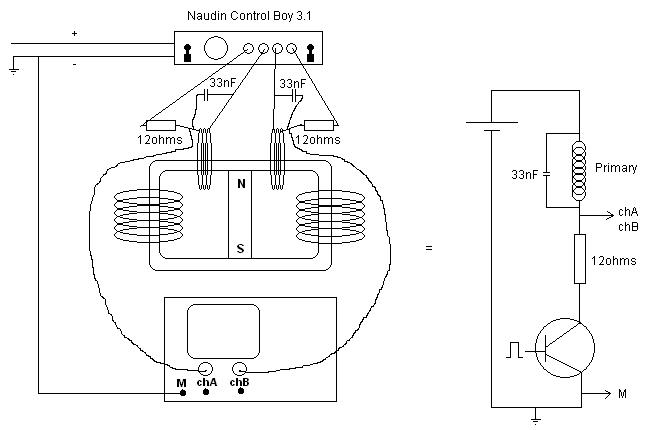
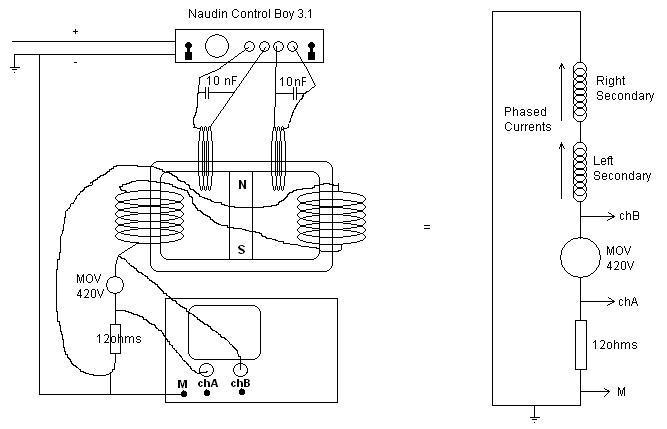
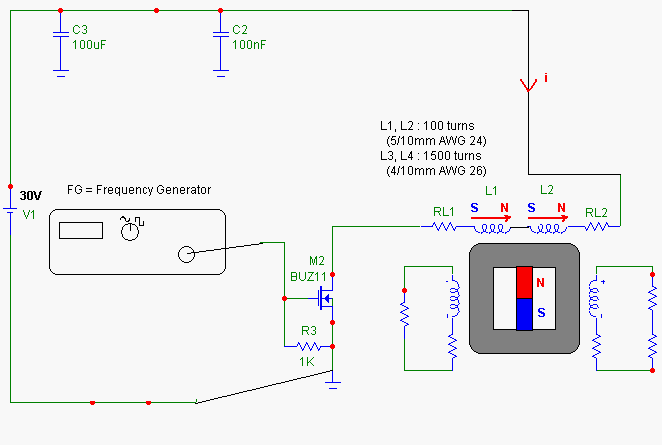
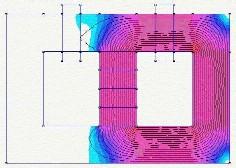
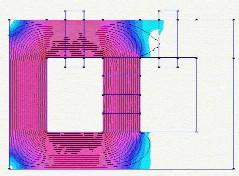
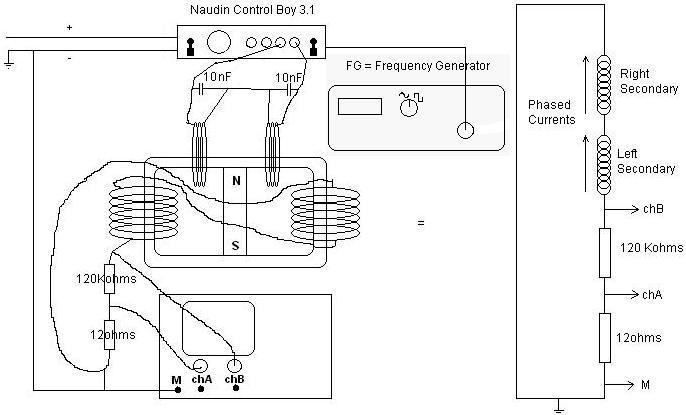
C’est un générateur électromagnétique sans partie mobile, qui comprend un aimant permanent et un cœur magnétique comprenant un premier et un second chemin magnétique. Une première bobine d’entrée et une première bobine de sortie entourent des parties du premier chemin magnétique, pendant qu’une seconde bobine d’entrée et une seconde bobine de sortie entourent des parties du second chemin magnétique. Les bobines d’entrée sont alternativement alimentées avec des courants pulsés pour produire des courants pulsés induits dans les bobines de sortie. La conduction du courant électrique à travers chacune des bobines d’entrée réduit un niveau de flux de l’aimant permanent à travers le chemin magnétique autour duquel la bobine d’entrée s’étend.
Dans une version différente du générateur électromagnétique , le coeur magnétique inclut des plateaux annulaires bien espacés, avec des poteaux et des aimants permanents s’alternant tout le long entre les plateaux. Une bobine de sortie s’enroule autour du long de chacun de ces poteaux. Les bobines d’entrée enroulées autour de parties des plateaux sont alimentées par des courants pulsés, induisant des courants dans les bobines de sortie.
…
Cliquez pour agrandir :
Comment acheter une machine à énergie libre ?
Bearden dit en 2000 : attendre 2003 à peu près ! En fait rien n’est jamais sorti, à date de 2025 toujours rien.
« Peut être que l’évènement le plus attendu en la matière est la commercialisation du Générateur électromagnétique sans mouvement (MEG) prévue pour commencer à peu près en 2003. C’est le moment où la preuve se fera aux yeux de tous. Beaucoup de personnes m’ont dit que, lorsqu’ils parlaient d’énergie libre, ils disaient « Je le croirai le jour où je pourrai l’acheter au magasin ». Si tout va bien, bientôt ils seront capables de commander leur propre MEG. Alors ils croiront, parce que ça marche et c’est en train de marcher.
J’avoue que le responsable scientifique d’un important groupe expérimental dans une grosse société a été plutôt assommé par le type de gain en sortie que nous sommes capables d’obtenir. Le MEG peut ressembler seulement à un transformateur, mais il n’en est pas un: il est de type complètement différent. »
D’après : http://www.cheniere.org/correspondence/011202.htm
« Bientôt les premières unités du MEG produiront 2,5 Kilowatts d’électricité gratuite, pour toujours. Les unités peuvent être connectées ensemble pour doubler ou tripler le wattage. Après que cette première phase, des générateurs de 10 kilowatts sont programmés. L’énergie s’écoulera librement dans le temps indéfiniment, et il n’y a aucune partie mobile à remplacer. Ce projet de manufacture est un effort héroïque et changera le monde tel que nous le connaissons. Pour une fois les gens seront en possession de dispositifs tels qu’il n’y aura plus aucun déni de quiconque, incluant en cela le gouvernement et/ou le gouvernement secret. »
D’après : http://www.prahlad.org(…)wars.htm
Ces promesses n’ont jamais été tenu, et les prévisions des kilowatts sortis est une caractéristique de tous ces systèmes à énergie libre quine marchent pas.
Pour analyser le MEG il faut le tester expérimentalement tel qu’indiqué. Il ne marche pas, mais une fois testé. Il y a malheureusement le pendant à la foule des menteurs qui inventent des fausses machines à énergie libre: les « zététiciens » qui se font appeler ainsi ou pas, et qui n’ont de cesse que de casser tout ce qui n’est pas conforme à leur dogme de croyance sans aucune critique fondée sur autre chose que « ce n’est pas possible car c’est débile, j’en ris », autant dire une haute analyse scientifique qui laisse pantoise de bêtise aggravée. Ce genre de personne se croit de plus scientifique en ne faisant rien que sortir du blabla.
Il y a aussi ceux qui sortent des arguments faux de mauvaise foi, qui sont balayés par l’analyse scientifique, tout ça aussi pour mettre au placard ce qui dérange.
Donc naviguer entre les escrocs des fausses inventions et les escrocs des dogmes zététiciens est difficile; la pratique est de jeter à la poubelle tous les dires et d’expérimenter pour tester et voir ce qu’il en est.
Analyse de la mauvaise foi des contradicteurs
Petit topo sur le MEG :
Le MEG semble décrié par un certain nombre de personnes, avec des arguments scientifiques de mesure à la clef; mais en les regardant de près, ils n’ont aucune validité.
| Exemple 1 | ||||||||||||||
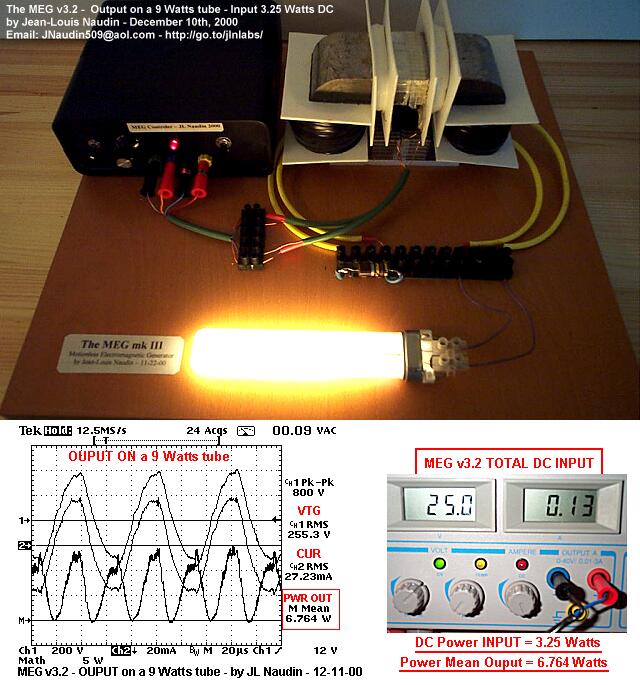
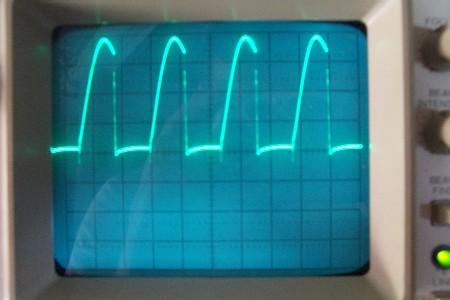
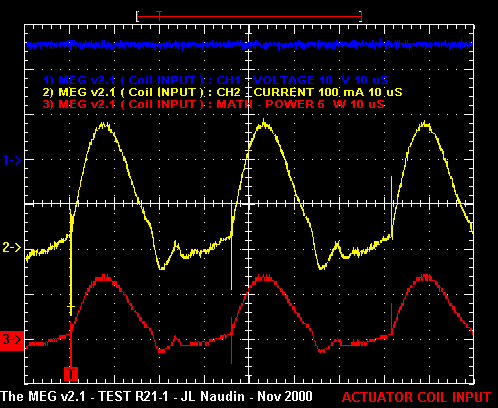
| Calculs volontairement faussésVoir ici les mesures de puissance d’entrée et de sortie du MEG 3.0 par Naudin:
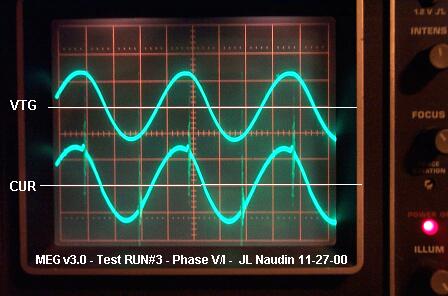
(les puissances sont calculées sans prendre en compte les valeurs efficaces) http://jnaudin.free.fr/meg/megv21.htm 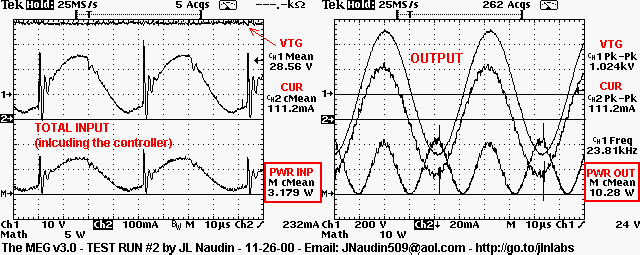 Image redimensionnée – cliquez dessus pour voir l’original en plein format Voir ici les calculs refaits en reprenant ces mêmes valeurs lues sur les graphes de Naudin: http://www.theverylastpageoftheinternet.com/magneticDev/meg/beardenmeg.htm Equations de base de l’électricité: (1) V = IR Loi d’Ohm 2) P = VI (puissance transférée) P = V²/ R = I²R (dissipation dans une résistance) Pour certains cas, ces équations s’adaptent; c’est le cas dans les circuits à courant alternatif, où il faut calculer la puissance moyenne, alors que ces calculs donnent la puissance instantanée. Lorsque la tension est constante et le courant alternatif sinusoïdal: (3) Pmoyenne = V (I0/ racine de 2) Si la tension et l’intensité sont alternatives: (4) Pmoyenne = V0²/ 2R (5) Pmoyenne = (V0 / racine de 2) (I0 / racine de 2) = V0 x I0 / 2 Données du MEG 3.0: Entrée: l’oscilloscope suggère 28V de tension constante. Le courant est alternatif (AC) d’amplitude I0 à peu près égale à 0.125A. Sortie: 500v sinusoïdal(pic à pic divisé par 2), 0.044 A. L’entrée est en courant AC (alternatif), on utilise donc l’équation 3: (3) Pmoyenne = V (I0/ racine2) Pentrée = 28 x 0.125 /racine de 2= 2.47 Watts La sortie est sinusïdale, donc on utilise l’équation 4. La seule chose à noter est que ça a été mesuré à travers une résistance de 100 kohms, et c’est ce qui doit être utilisé dans les calculs, et comme il y a deux bobinages de sortie, on multipliera le résultat par 2 (4) Pmoyenne = V0² / 2R Psortie = 500² / 2 * 1000000= 1.25 Watts Psortie totale= 2.50 Watts coefficient d’efficacité (COP) final du MEG 3.0= 2.50 / 2.47= 101% Là où ce calcul n’est pas valide, c’est que Naudin n’a jamais dit que la tension de 500V était mesurée aux bornes d’une résistance de 100Kohms. On peut appliquer Pmoyenne = V0²/2R lorsque V0 est la tension appliquée aux bornes de la résistance R. Naudin précise seulement qu’il utilise une résistance de 100Kohms; mais il peut très bien avoir utilisé un pont diviseur de tension et donc appliqué une tension inférieure aux bornes de la résistance ou autre chose. Il n’est pas assez clair sur ses techniques de mesure, c’est sûr, pas assez transparent.
Ce qui est à prendre en compte, ce sont les résultats des courants et tensions circulant dans la charge qu’il a utilisé pour sa mesure. Ils apparaissent sur le graphique, et on utilise alors l’équation (5) donnée gentiment par notre dé-crieur: Pmoyenne = = V0 x I0 / 2 = 500 x 0.44 / 2 = 7,8 watts et là on ne sait pas si Naudin a mesuré la puissance totale des deux bobines ou d’une seule mais si c’est d’une seule il faut encore multiplier ce résultat par deux. Mais en en restant là on obtient un COP de 3,16 soit 316%. Pour savoir ce qui a été réellement mesuré, il reste à refaire l’expérience soi même ou demander le détail à JL Naudin qui a beau avoir mis des tas d’informations sur le MEG dans son site, n’a pas expliqué ses protocoles de mesure; il a seulement donné des relevés de mesure.
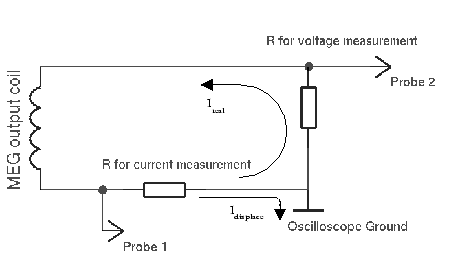
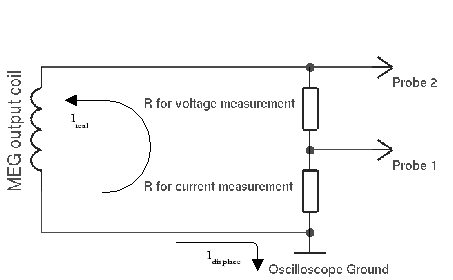
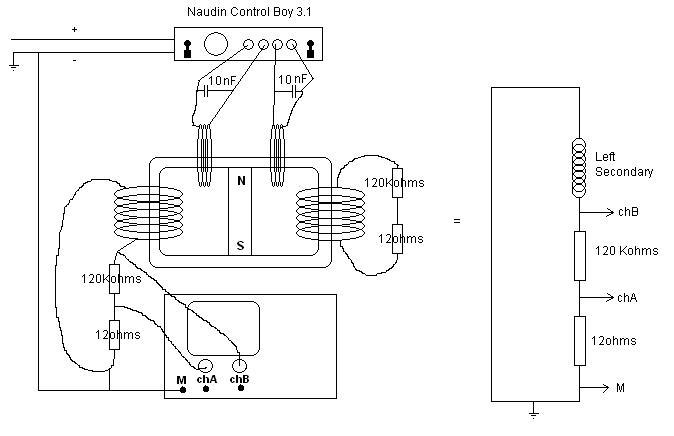
Les critiques disent que le montage utilisé mesure un courant qui va à la masse de l’oscillo en plus du courant qui boucle dans la bobine, ce qui ajoute faussement de la puissance au MEG. Voilà où serait le point de mesure:
Voilà où il devrait être pour que la mesure soit correcte:
Le problème est que Bearden n’a fourni nulle part de plan indiquant où il fait ses points de mesure, et ces critiques sont de pures spéculations. Encore une fois, comme Bearden fait de la rétention d’informations pour des raisons commerciales (il compte sortir un MEG à la vente); il en dit le moins possible sur les aspects pratiques du montage (que Naudin a reproduit comme il lui semblait, mais sans savoir vraiment non plus). Alors c’est encore de la pure critique
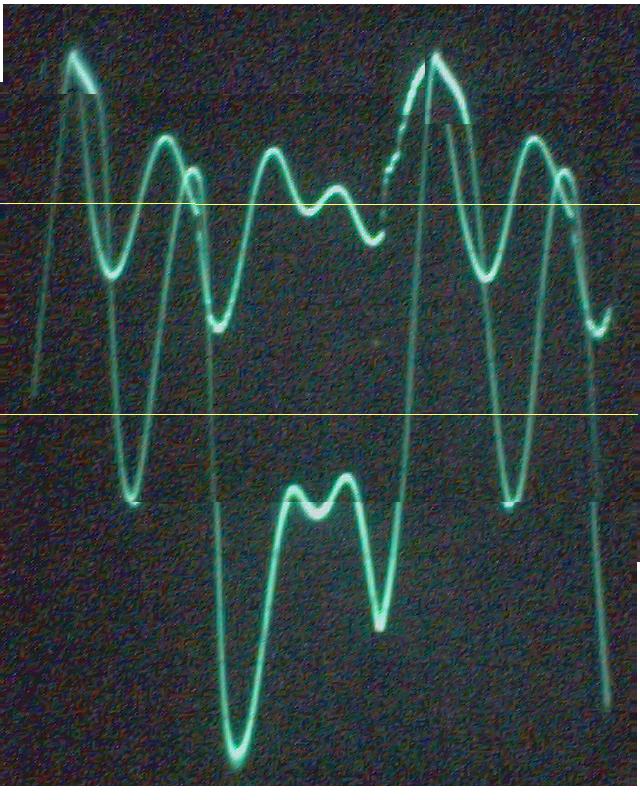
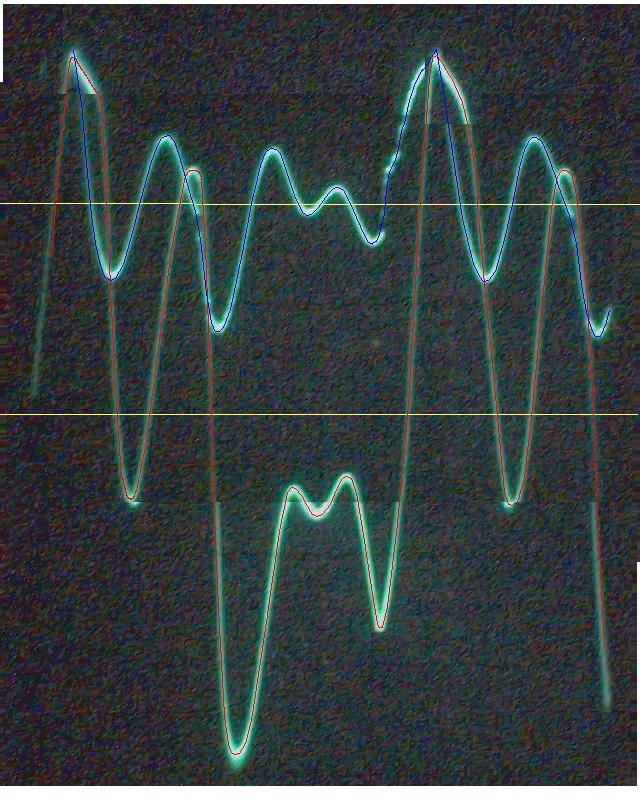
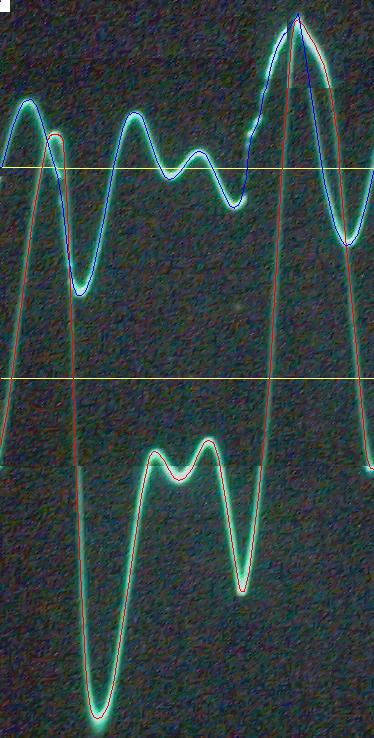
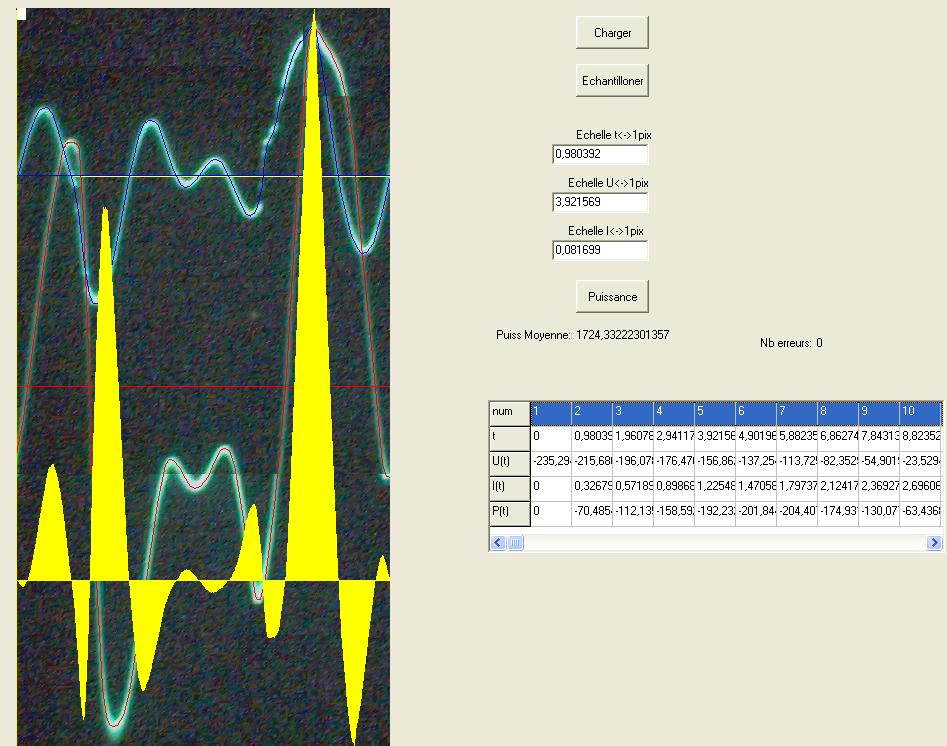
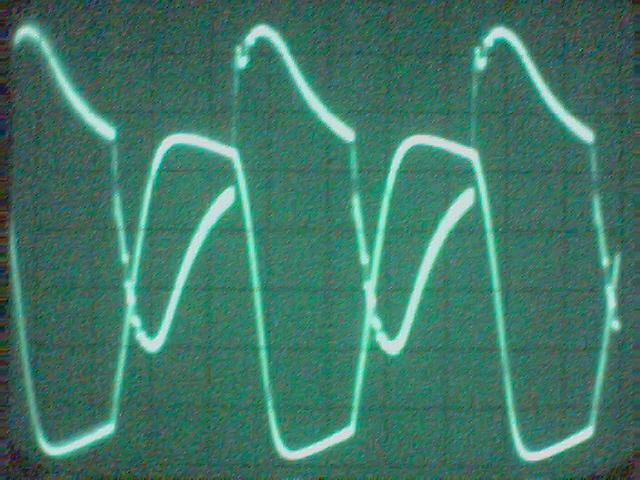
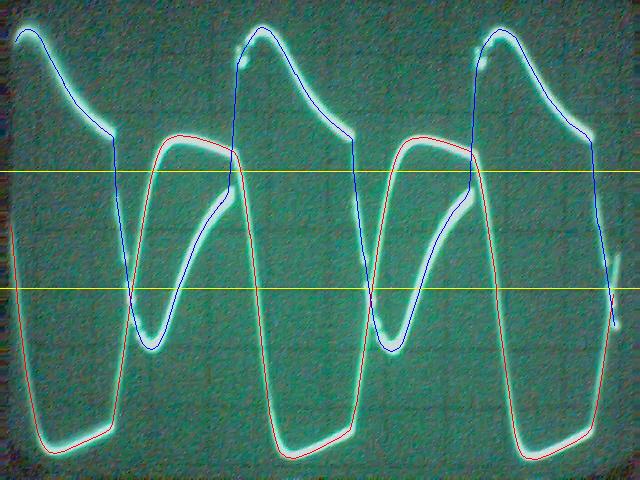
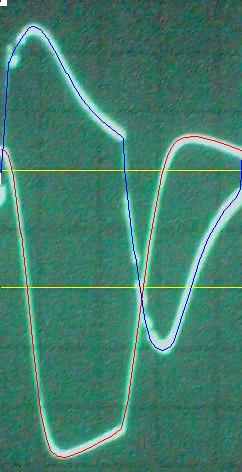
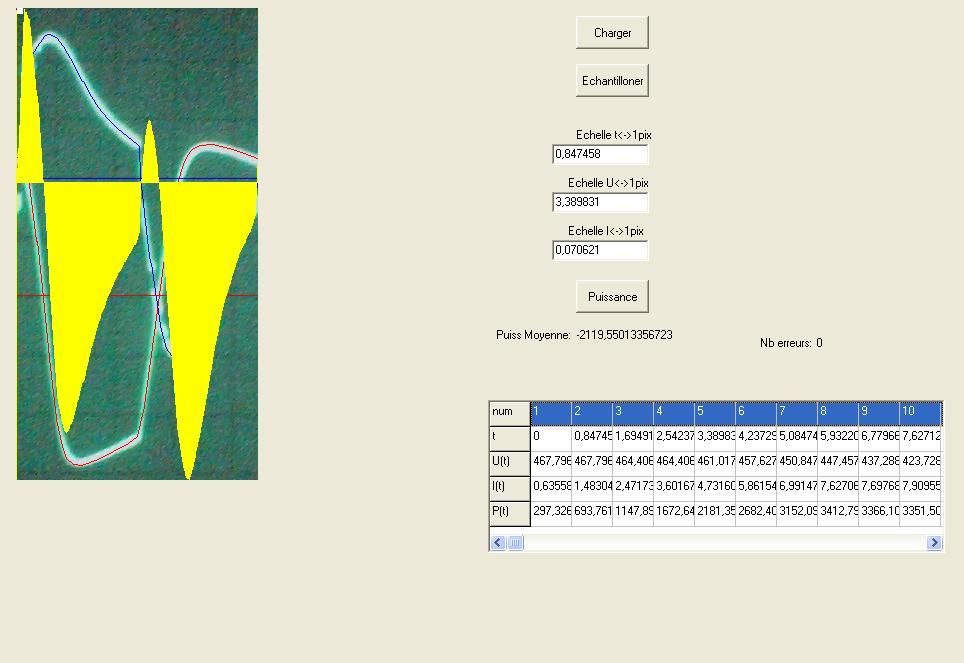
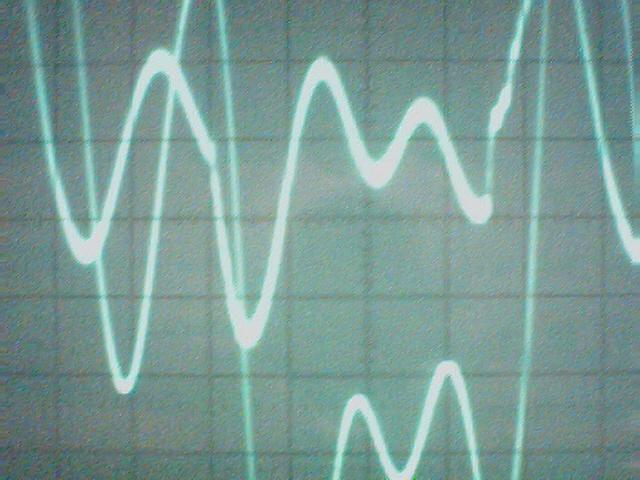
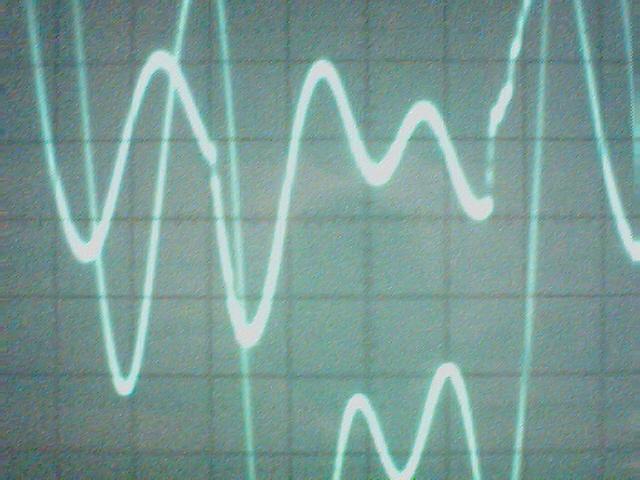
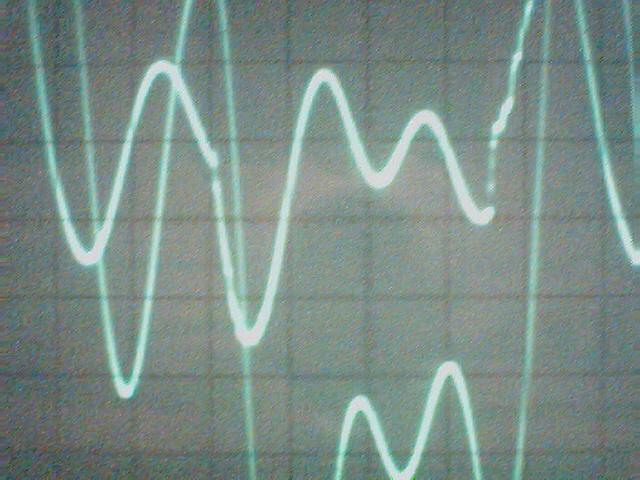
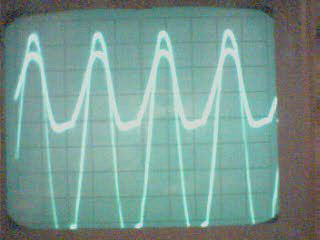
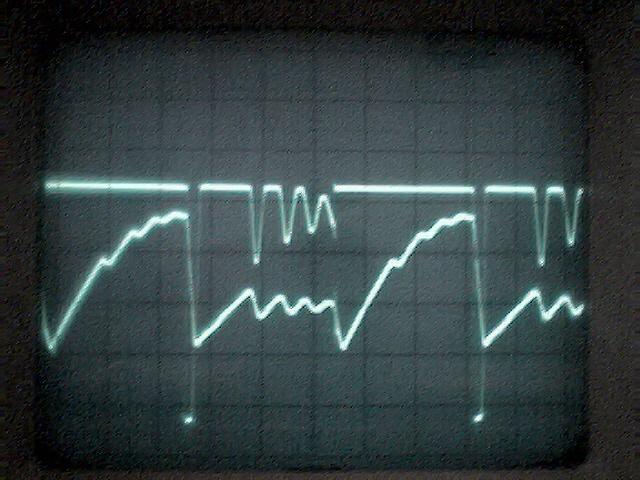
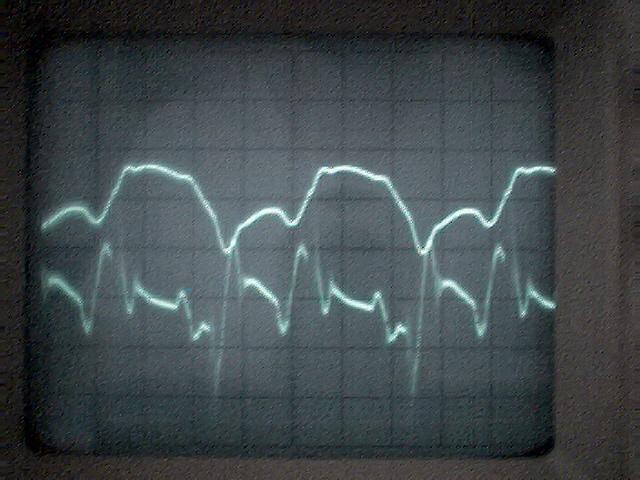
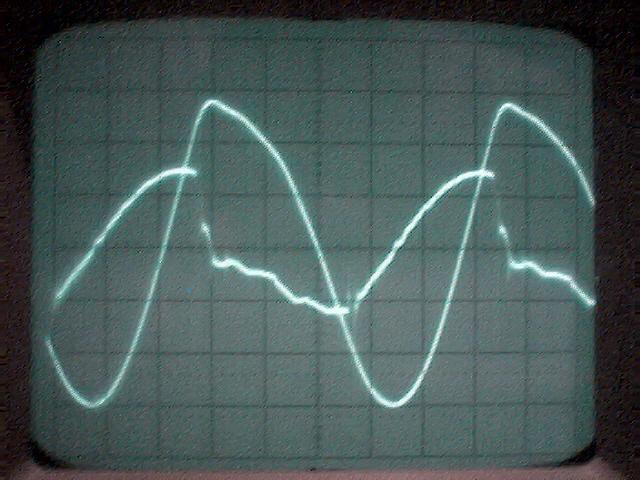
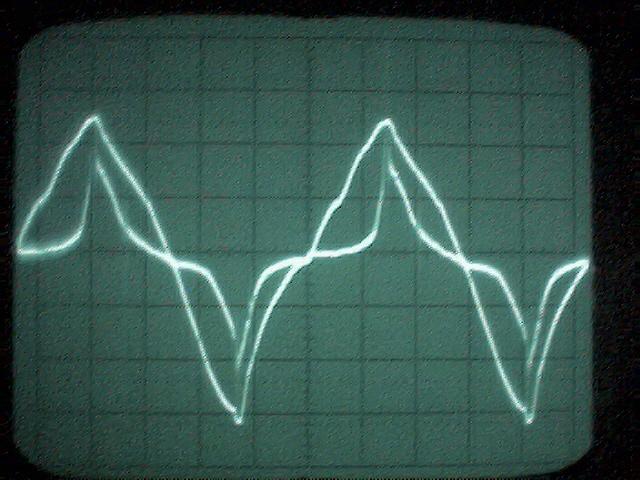
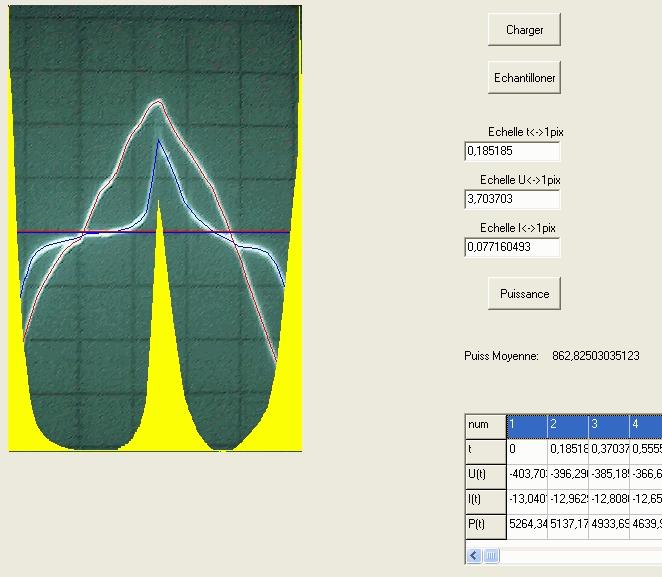
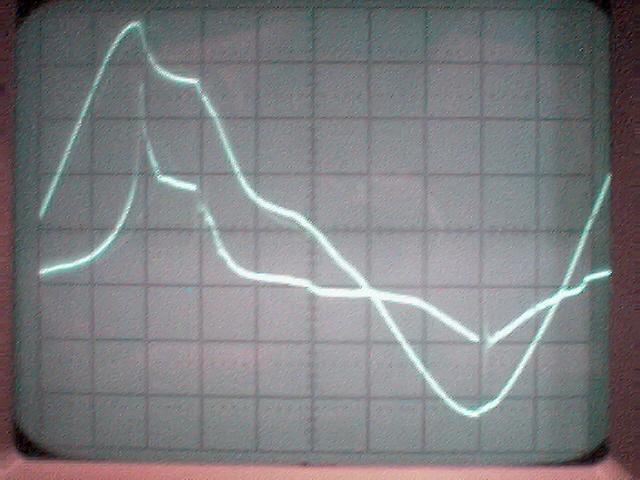
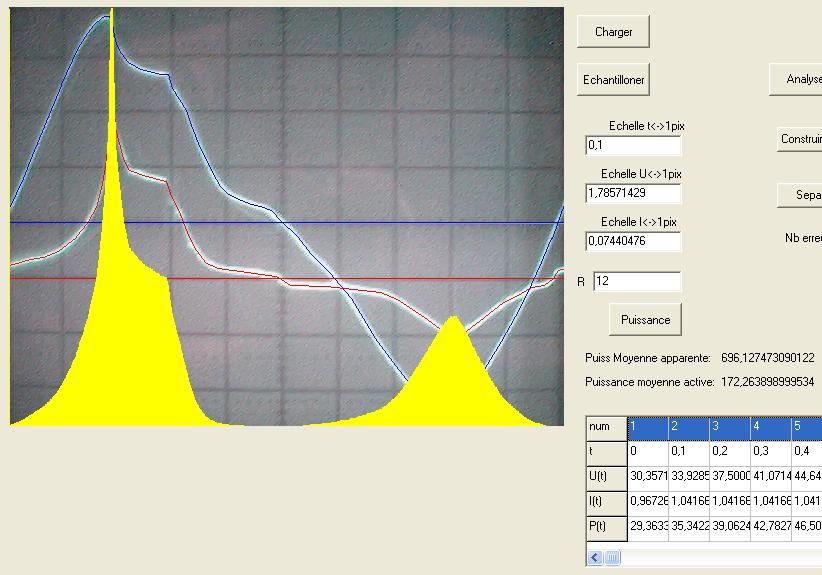
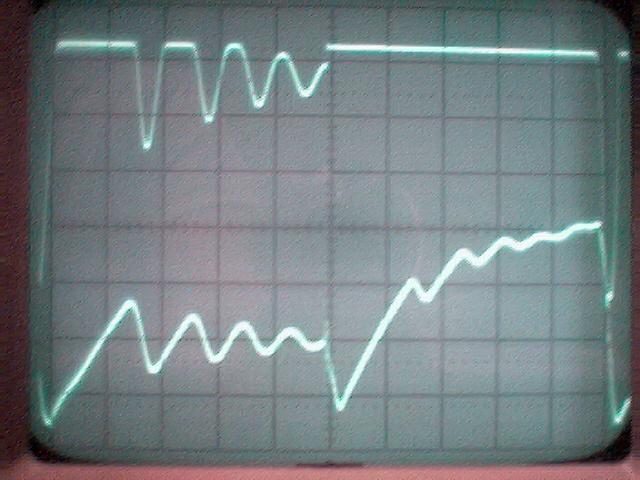
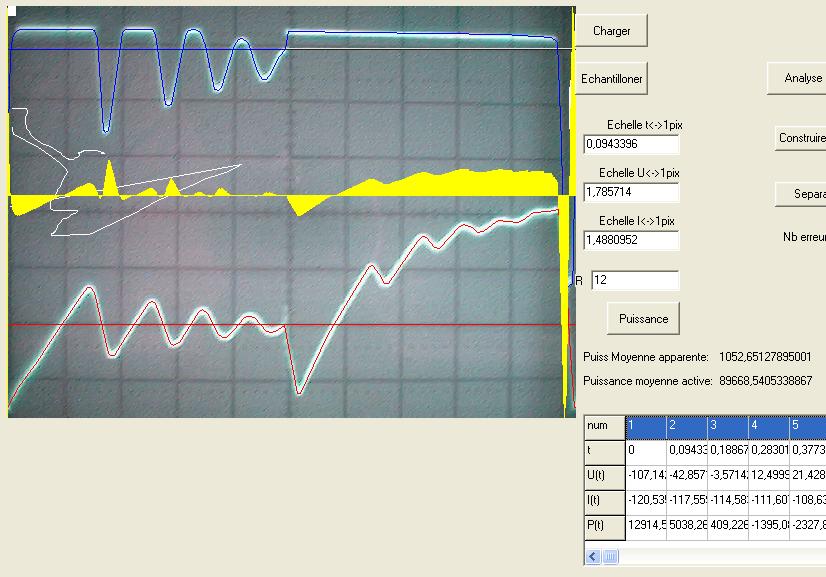
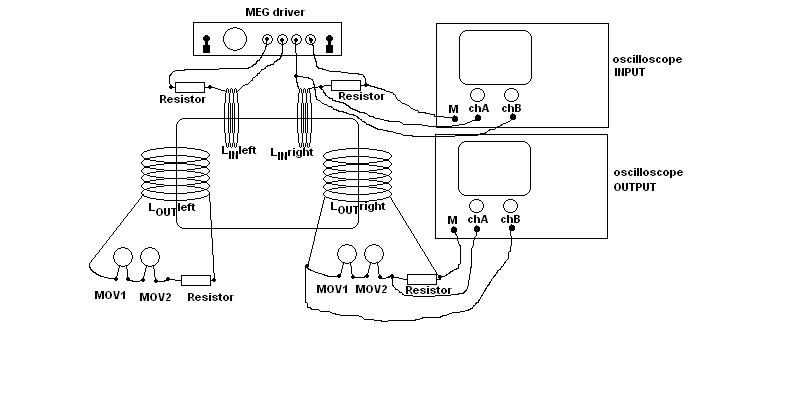
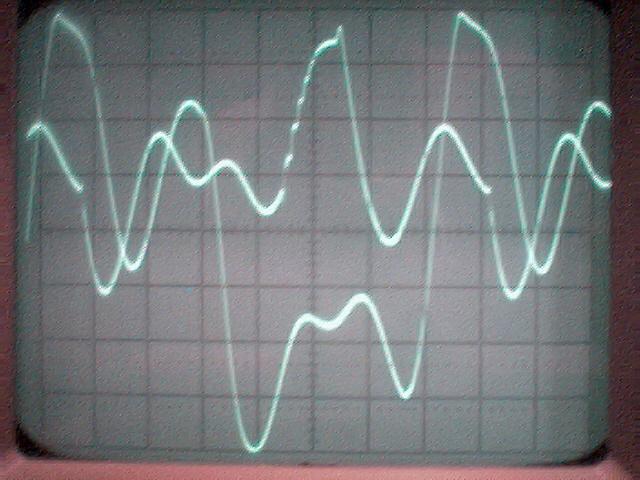
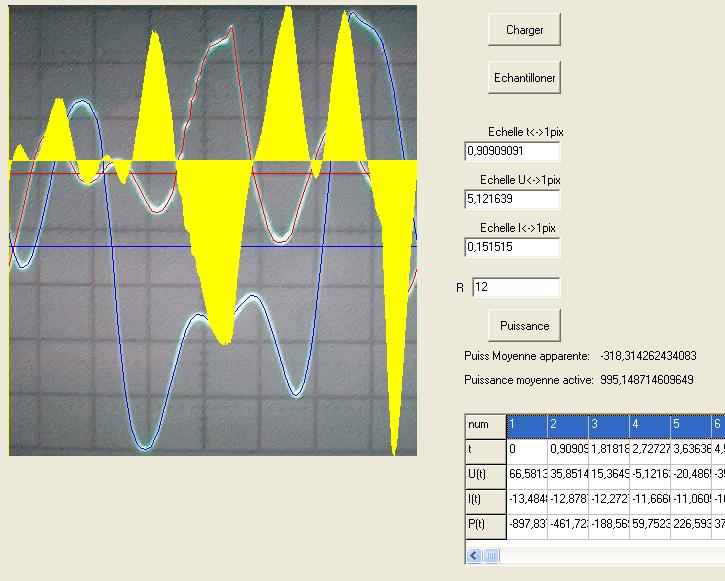
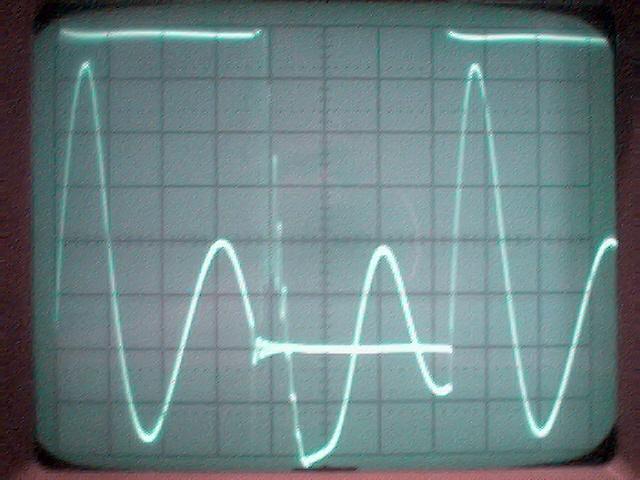
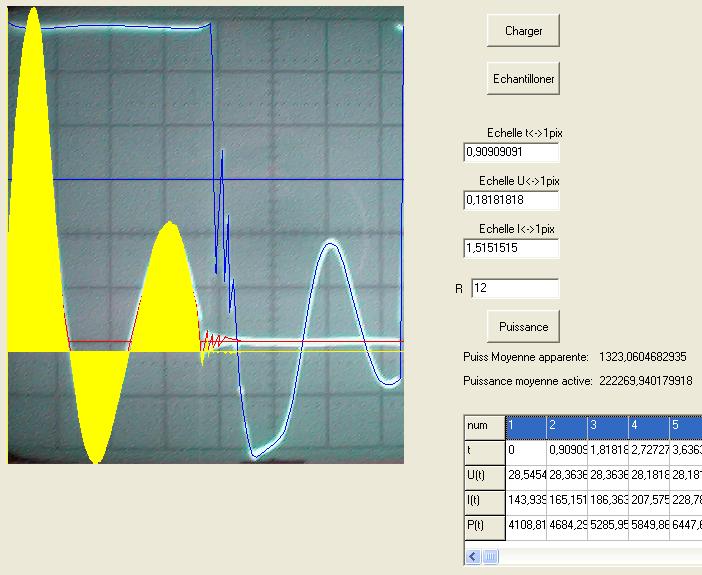
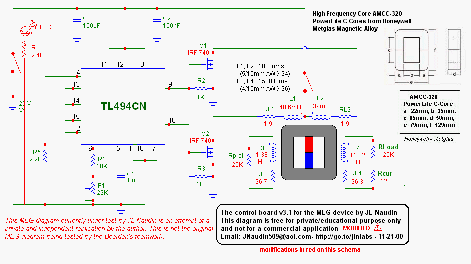
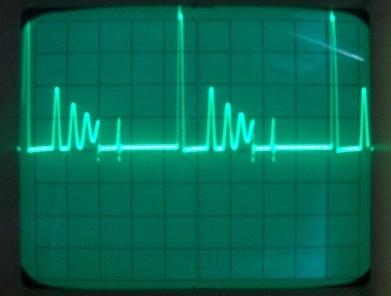
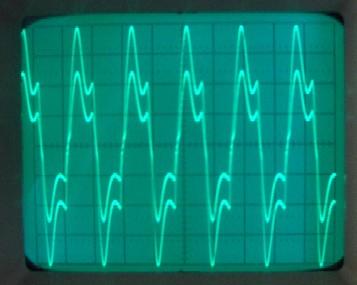
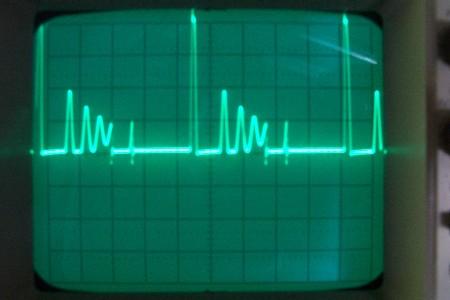
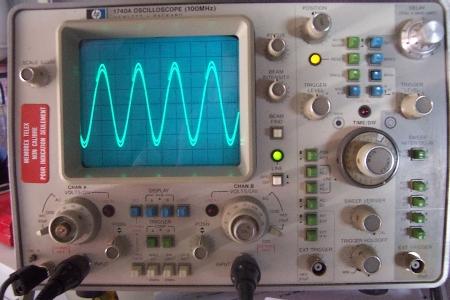
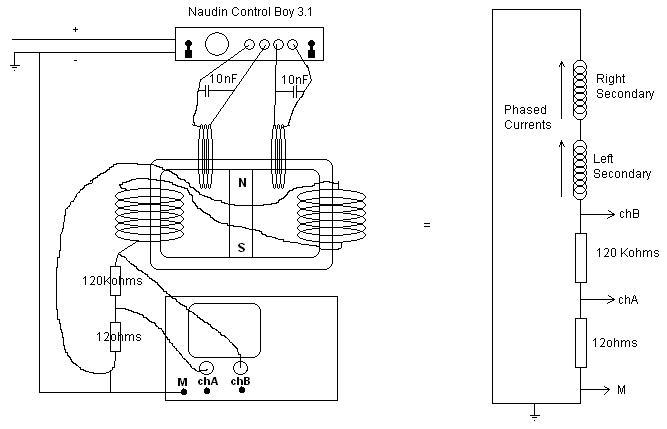
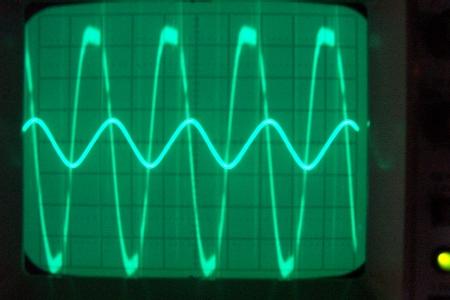
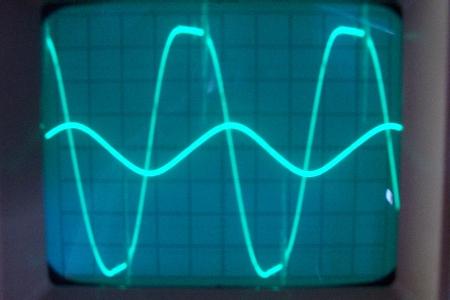
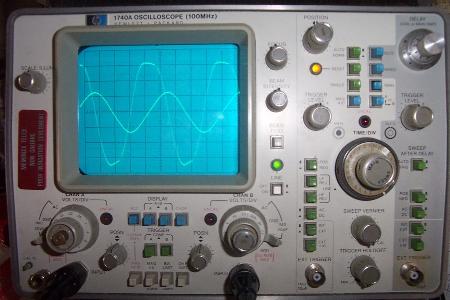
La conclusion qui s’impose est que décidément, on a très peu d’information sur ce MEG et les mesures de puissance. Il semblerait toutefois que Bearden se soit emballé, car il pensait pouvoir produire des COP aussi grands que voulus pour produire des MEG de très forte puissance; et finalement il semblerait qu’un COP de 5 est attendu. Mais en enchaînant en série plusieurs de ces MEG, on augmente la puissance significativement, et on peut effectivement arriver à produire énormément. Pour répondre à la question: le MEG marche-t-il, finalement, il ne faut pas lire la littérature de Bearden ou de Naudin ou de leur détracteurs, mais en construire un! Si vous voulez voir des joutes scientifiques basées sur le vide et la certitude que ça ne fonctionne pas, sans faire plus que cela, il y a aussi: —– Notes appendices à l’Exemple 1: Il semble que, si la mesure s’est bien faite à travers une résistance de 100Kohms directement, sans autre complexité du montage, elle soit faite à travers une résistance « conditionnée » selon les termes de Naudin. Il explique ce que cela veut dire, et en fait cela consiste à transformer la résistance en varistance, dont la résistance varie avec la tension appliquée: http://jnaudin.free.fr/html/negres.htm Donc, la valeur de la résistance à 500V n’est plus de 100 kohms, les calculs du sieur de l’exemple 1 sont donc faux de manière flagrante. La raison de l’utilisation d’une varistance est donnée ici: http://jnaudin.free.fr/meg/megnot01.htm En tous cas, le détracteur n’a pas pris du tout ceci en compte, comme le font les détracteurs malhonnêtes le plus souvent. La preuve que je ne suis pas le seul à penser ainsi, je l’ai eu en trouvant cette page, après coup: http://jnaudin.free.fr/meg/criticofsb.htm Le MEG : Expériences de 2004 Note de 2006: Les expériences de 2004 que vous allez lire dans les pages qui suivent sont entachées de plusieurs erreurs de mesure pour commencer, jusqu’à arriver à la conclusion que le MEG ne fonctionne pas du tout en surunité une fois les mesures effectuées dans les règles de l’art électronique. De plus un montage incorrect des bobinages n’aurait pu permettre la surunité si cela avait été possible. Je vous conseille directement de lire les expériences de 2005 plus loin. Je laisse celles de 2004 comme archives historiques lorsqu’on apprend à mesurer correctement en commençant par se tromper! Grâce à littlemat qui m’a prêté un MEG qu’il a fait monter par un ingénieur en électronique pour des tests, et avec le concours de pascal pascal et moi avons fait des mesures infructueuses sur le MEG que nous avons en prêt, il y a quelques jours.Après études complémentaires des défaillances possibles et erreurs de montage, informations précises récoltées sur le groupe des constructeurs de MEG à l’adresse: http://groups.yahoo.com/group/MEG_builders/ et à l’aide des commentaires de Bearden et de Naudin pour conseiller d’autres personnes, deux rectifications ont été faites (une sur les aimants, et une autre sur la fréquence d’accord du circuit). S’en suit ce qui semble être un succès ce soir, je dis ce qui semble car il faut des calculs complémentaires pour confirmer ou infirmer les résultats, étant donné la nature alambiquée des signaux de sortie; mais c’est vraiment un premier pas qui met motive à souhait!!Voilà les mesures effectuées, qui donnent à l’heure actuellement COP=2,2 soit 220% d’efficacité (ramené à COP=3,4 soit 340% d’efficacité si on mesure seulement la consommation du MEG et pas celle du circuit attenant)J’espère seulement que le prochain message de calcul précis du COP avec méthodes numériques donnera confirmation de ces résultats et n’annoncera pas que ceci était de faux espoirs!!Une remarque: les premiers tests il y a quelques jours donnaient une efficacité de 25% (en clair on perdait les 3/4), et on ressentait une énorme émission d’ondes électromagnétiques sur la peau (confirmée par un petit champ mètre très grossier): voilà où partaient les 75% de perte je pense. Dans les expériences de ce soir (que j’ai dû abréger, aussi elles ne sont pas complètes, une seule l’est) je ne ressentais plus cette émission du tout (mais je n’ai pas fait de mesure). Il faudra vérifier la pollution électromagnétique du MEG (si on se procure de l’énergie au prix d’un cancer pour exposition à des champs électromagnétiques intenses sur longue durée on n’a rien gagné). Par contre pour la pollution sonore c’est perdu: un bruit strident (de 3KHz je pense, fréquence des impulsions émises) se fait entendre lors du fonctionnement du MEG de ce soir.Voilà le compte rendu détaillé de ce qui a été fait ce soir: (PS: désolé pour les photos basse qualité, mais n’ayant pas d’appareil numérique, j’ai utilisé ma webcam, qui est assez pourrie!!)MEG adapté de la version 3.1 de JL Naudin Expériences du 07/03/2004 vers 19h00 France (dép 77)Bobinage n°1 (bobinage gauche): connecté sur Résistance 1MOhms Bobinage n°2 (bobinage droite):VDR1 = VDR2 = 420V / 400pF Rch = résistance 12ohms, 10Watts Bobinage n°2 U1 _______mmmmm_______ U2 | | ———–VDR1–VDR2-*-Rch—– | | | sB sA | | | | CHB CHA masse *: point de mesure entre VDR2 et Rch sB: sonde B reliant U1 à CHB sA: sonde A reliant * à CHA CHB: sur oscillo ( mesure la trension aux bornes de la bobine: V=tension entre U1 et U2) CHA: sur oscillo ( mesure la tension aux bornes de la résistance de charge Rch, pour mesurer le courant I qui parcourt le circuit, pertes de courant par CHA et masse oscillo négligées ) ___________________________________________________________ mesure capacité VDR1+VDR2 : C=200pF mesure inductance Bobinage n°2: L=12,8 Henrys résonance estimée à: 1/(2 x pi x square (LC)) = 3,1KHz (estimation seulement car sB et sA, ainsi que l’oscillo ont des capacités parasites) d’où modification du circuit Naudin MEG 3.1 par adjonction d’une capacité de 10nF en parallèle sur le 1nF de réglage de la fréquence des impulsions du TL494CN. Gamme de fréquence alors disponible: 1,6KHz à 5,5KHz environ ___________________________________________________________ sB: rapport de tension de mesure 10:1 sA: rapport de tension de mesure 1:1 CHB: 0,1 Volts/Division, 0V sur la ligne du bas du schema reference.jpg CHA: 20 Volts/Division, 0V sur la ligne du haut du schema reference.jpg Base de temps: 50 micro secondes/Division  Tension générateur alimentation du montage, à vide: Ugen=29,4V Courant générateur alimentation du montage, à vide: Igen=0,04A Pconsommée à vide gén= 1,2 Watts (le max et le min dépassant l’écran, j’ai dû déplacer la position du zéro et prendre un point de référence pour la lecture des crêtes de tension) —————- 1ère expérience: —————- Tension générateur alimentation du montage: Ugen=28,6V Courant générateur alimentation du montage: Igen=0,12A CHB: 12 divisions crête à crête, soit 12 x 20 = 240V mesurés sur CHB, soit 240 x 10 = 2400V entre U1 et U2 (sB en 10:1) CHA: 3 divisions crête à crête, soit 3 x 0,1V = 0,3V mesurés sur CHA entre * et U2 estimation de la période: 6,3 divisions, soit 6,3 x 50 micro sec = 315 micro sec <–> 3,2 KHz Vcrête à crête = 2400V I crête à crête = courant correspondant à 0,3V sur une résistance de 12 ohms, soit 0,3 / 12 = 25mA signaux V et I en phase: angle theta=0° (non sinusoïdaux, difficile à estimer, mais maxima et minimas atteints en même temps) Vmax=Vcrête à crête/2 = 1200V Imax=Icrête à crête/2 = 12,5mA Pmesurée = cosinus (angle theta) x Umax x Vmax / 2 = Umax x Vmax / 2 = 1200 x 0,0125 = 7,5 Watts Pfournie gén = 28,6 V x 0,12 A = 3,4 Watts soit COP = 2,2 (et si on tient compte seulement de la puissance consommée par le MEG et pas le circuit, on a: Pconsommée MEG = Pfournie gén – Pconsommé à vide gén = 3,4 – 1,2 = 2,2 Watts alors COP = 3,4) Il faut calculer numériquement Pmesurée par calcul numérique en traçant la courbe de U x I instantané, puis en intégrant numériquement sur une période pour avoir Ptotal, pour ensuite calculer la puissance moyenne sur cette période en divisant Ptotal par la longueur de la période pour avoir une valeur exacte de P même si le signal n’est pas sinusoïdal (tous les calculs précédents sont basés sur U et I sinusoïdal, ce qui n’est pas du tout le cas, donc calculs à faire pour avoir une vraie mesure du COP) —————- 2ème expérience: —————- Tension générateur alimentation du montage: Ugen=29V Courant générateur alimentation du montage: Igen=0,07A Dans les mêmes conditions, fréquence des impulsions modifiée (au maximum soit environ 5,5 KHz) Pas de lecture crête à crête de CHA ni CHB manuelle, lire sur le graphique capturé par webcam —————- 3ème expérience: —————- Tension générateur alimentation du montage: Ugen=29V Courant générateur alimentation du montage: Igen=0,07A Dans les mêmes conditions, fréquence des impulsions modifiée (au minimum soit environ 1,6 KHz) Sauf modifié base de temps, positionnée sur 0,1 milli secondes. Pas de lecture crête à crête de CHA ni CHB manuelle, lire sur le graphique capturé par webcam Il semble qu’il y ait un pic de consommation de courant (et aussi de puissance donc, vu que la tension d’entrée est presque constante pour f = 3,2Khz, qui doit être la fréquence de résonance du circuit de mesure sur le bobinage n°2) Suite de l’expérience: calcul précis de la puissance de sortie par calcul numérique Après études numériques longues et fastidieuses dont le détail va suivre, la conclusion est que les calculs estimés précédemment pour les signaux sinusoïdaux sont complètement inadaptés: la puissance calculée est de 1,84 Watts (calculs aux erreurs de lecture et d’approximation de la courbe, 10% d’erreur maxi) d’où COP = 0,54 ou en tenant compte seulement de la consommation du MEG et pas du circuit à vide COP=0,84 Donc c’est le bide complet!!! Notes: -Penser à écrire un programme qui effectue tout le calcul manuel que je me suis tapé pour arriver à ça pour les prochains essais de mesure de puissance, parce que là y en a marre de calculer! -Penser à ne plus jamais utiliser de formules pour signaux sinusoïdaux lorsqu’ils ne le sont pas!! Bon, déception, mais on est à mieux que les 25% du début quand même. Mais enfin pas de sur-unité, sniff!! On va pas se laisser décourager et continuer d’arrache-pied, suite au prochain épisode. Voilà les détails: D’abord traiter la capture de la webcam avec Paint pour repasser les séparateurs de carreaux de l’oscilloscope: 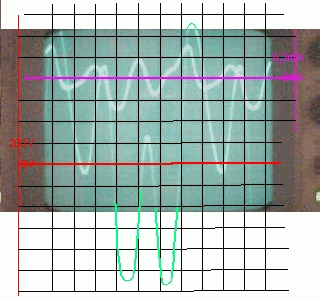 Puis imprimer et retracer à la main les courbes de l’intensité et la tension en rouge et bleu, ainsi que choisir une période du signal sur laquelle faire les calculs, et la diviser en un découpage par pas (lignes vertes verticales): 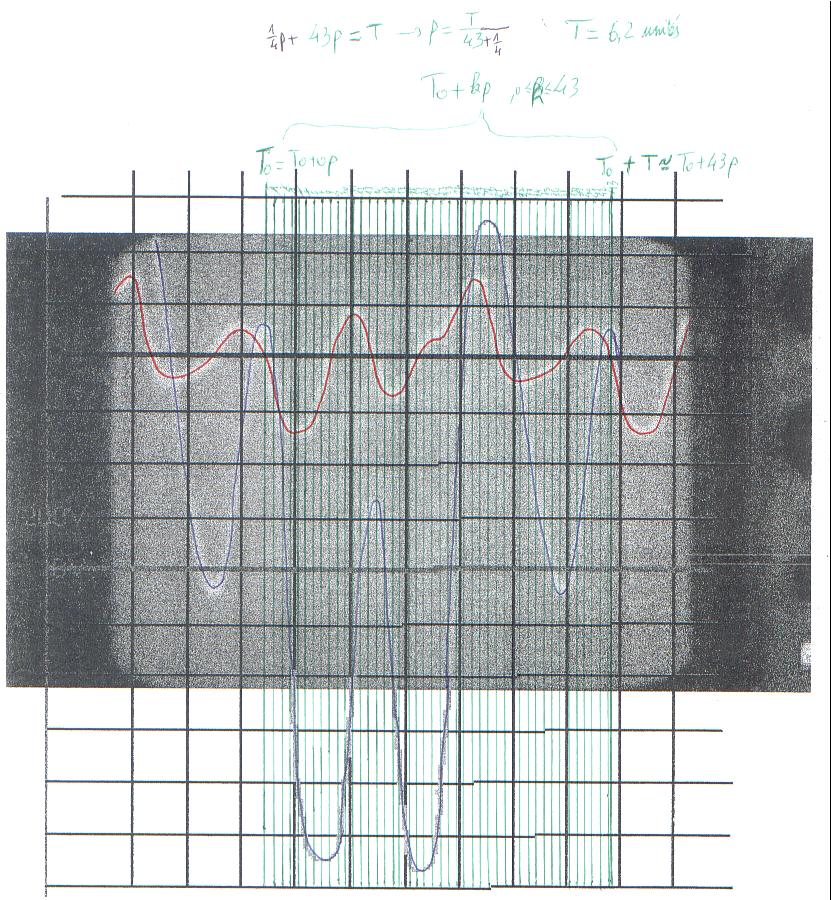 Après cela mesurer les distances en cm sur ces courbes, et convertir les distances mesurées en mA (intensité) et Volts(tension), ainsi que les temps en micro secondes: 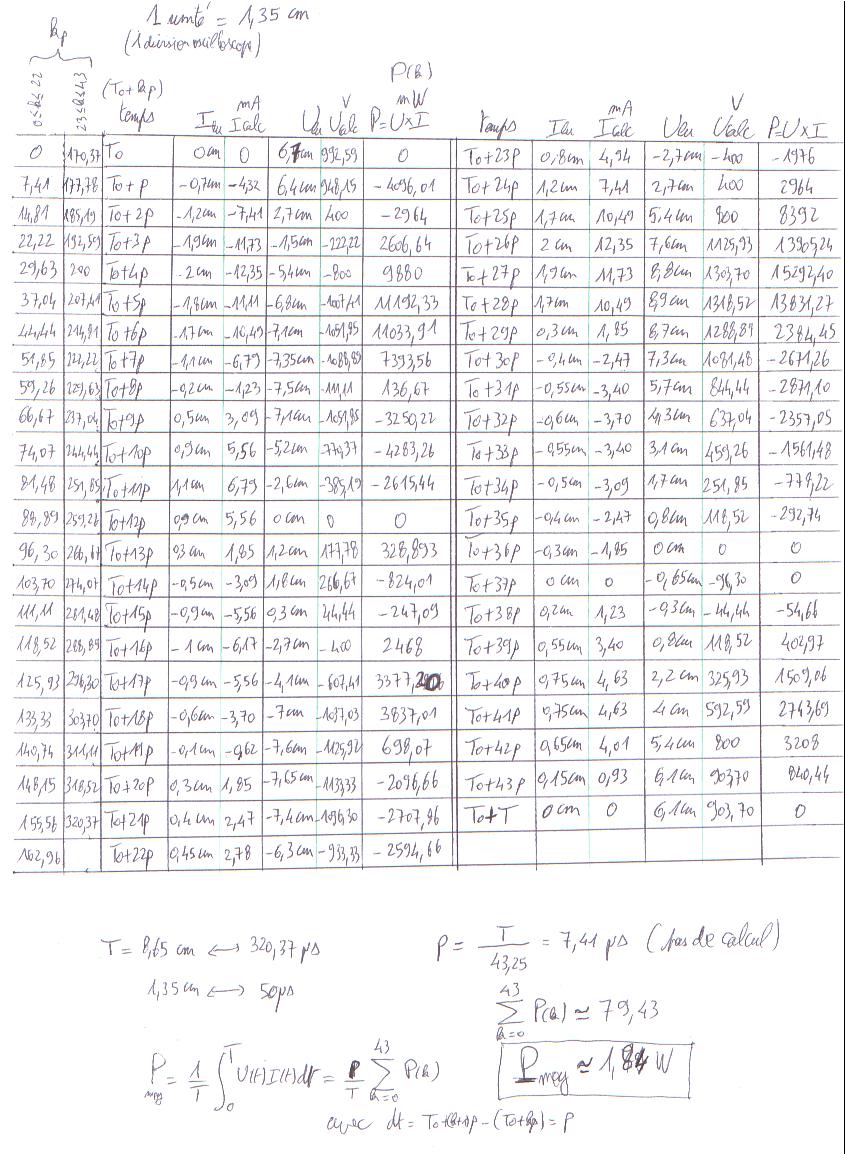 Saisir le tout (en convertissant les puissances de la feuille de calcul qui étaient en milliwatts, vers de watts) sur un logiciel grapheur de nuage de points: 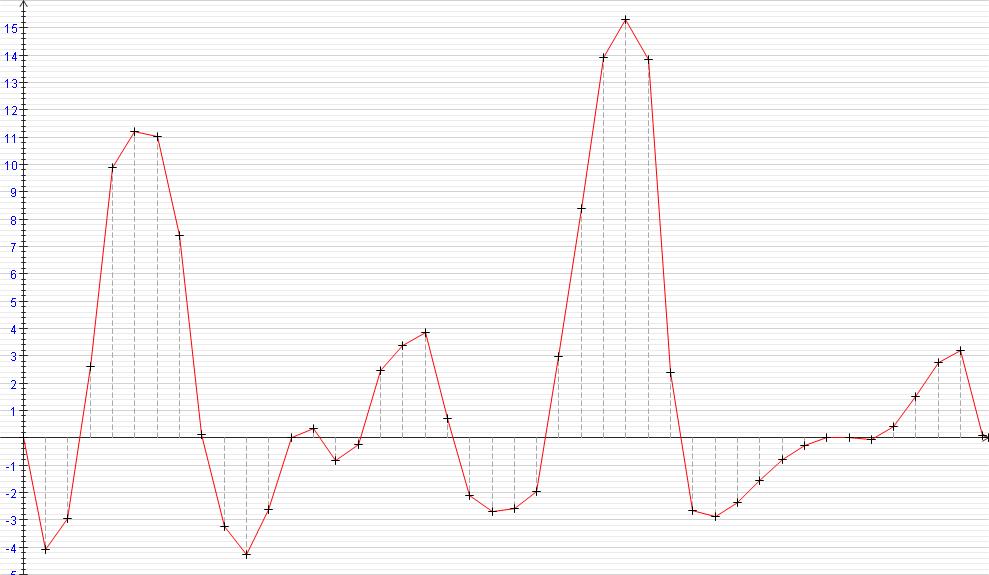 Puis, saisir le tout sur une feuille Excel et faire le calcul de la puissance moyenne sur la période: (calcul de l’intégrale de la puissance puis division par la longueur de la période, donc calcul de l’aire moyenne sous la courbe de la puissance): 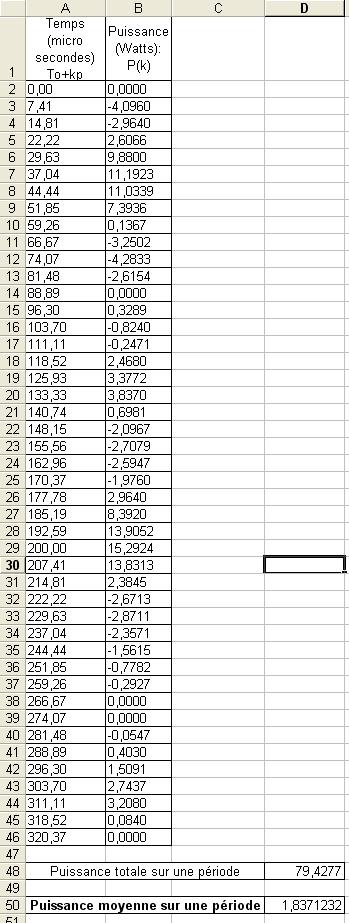 Et voilà le résultat: Pmoyenne = 1,8371232 Watts sniff! Bon, une autre idée: j’ai utilisé seulement une sortie du MEG, sur les deux sorties. Or, j’alimente le MEG avec les deux entrées, donc à bloc. Du coup, si je mesure la puissance sur les deux sorties au lieu d’une, est-ce que je mesurerai 2 fois 1,84 Watts? Auquel cas là on serait sur unitaire (même pas trop mal puisque la consommation réelle du MEG est de 2,2Watts, car le circuit d’alimentation de l’électronique consomme 1,1Watts à vide, donc il ne faut pas vraiment compter les 3,4Watts d’entrée au total). Mais peut être une mauvaise surprise attend les intrépides expérimentateurs si en mesurant sur les deux sorties les puissantes sont réduites par deux (enfin je ne vois pas comment mais on ne sait jamais….) Et puis aussi relier les deux sorties ensemble en série et voir ce que ça donne. au TAF!! — MEG adapté de la version 3.1 de JL Naudin Expériences du 11/03/2004 vers 17h00 France (dép 77) Bobinage n°1 (bobinage droite): montage identique au bobinage n°2 Bobinage n°2 (bobinage gauche):
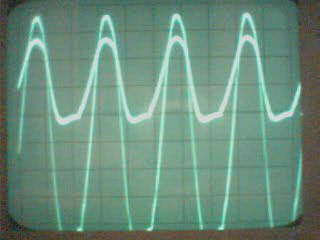
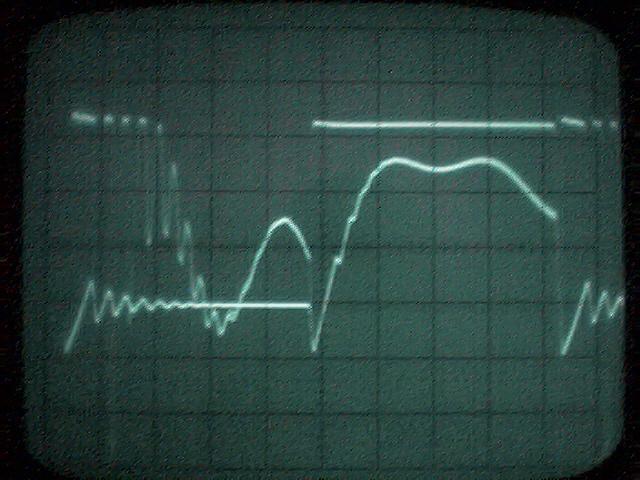
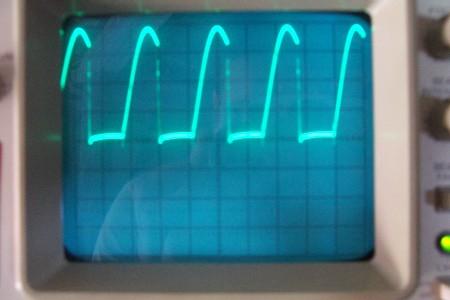
chA= 1,67mA/div, chB=200V/div, Cliquer pour agrandir 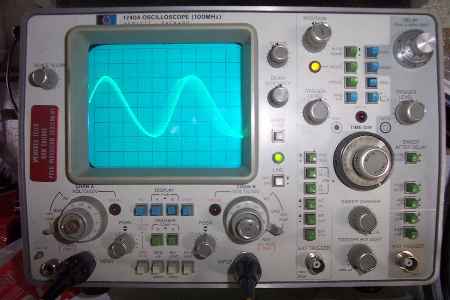 Je n’ai affiché que la tension, car la tension et le courant étaient en phase et en rapport du pont diviseur de tension 120Kohm/12ohm 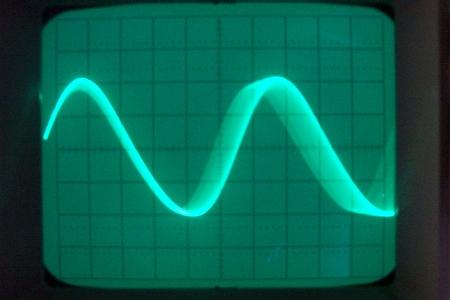 Puissance de sortie = Pout= U²/(2xR) = 400²/(2×120 000) = 0,67 Watts COP = 0,32 2) Signal sinusoïdal injecté J’ai recherché la fréquence de résonnance du courant, pour avoir un courant maximal.
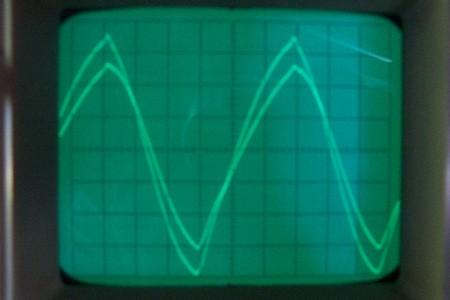
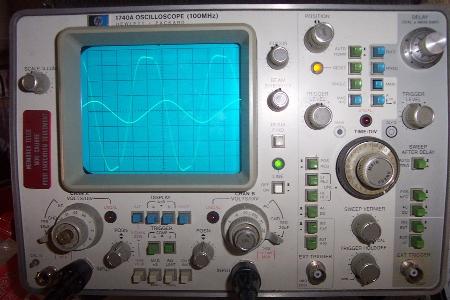
 Alimentation:  Pin = 3.9Watt
|
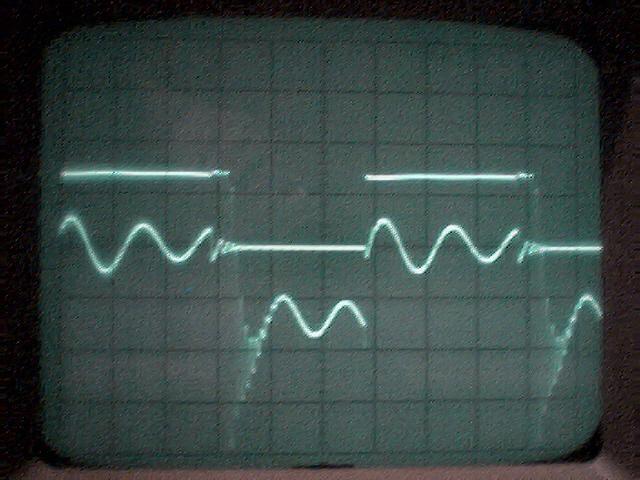
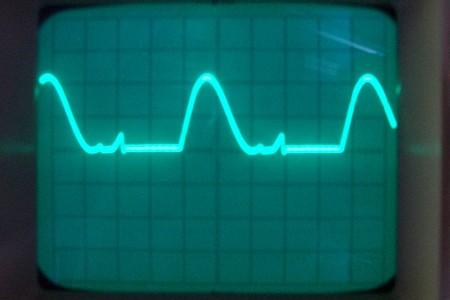
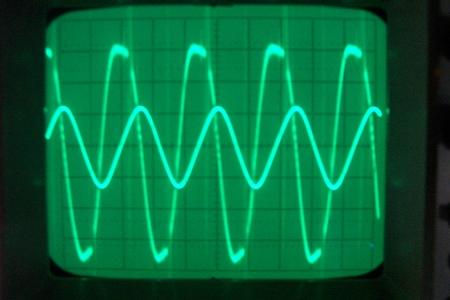
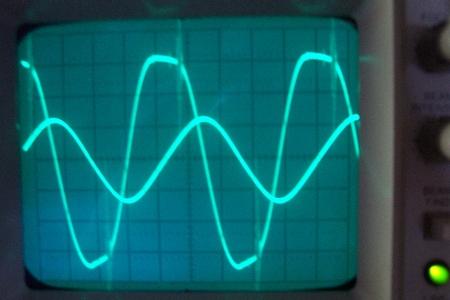
chA= 1,67mA/div, chB=200V/div, Cliquer pour agrandir

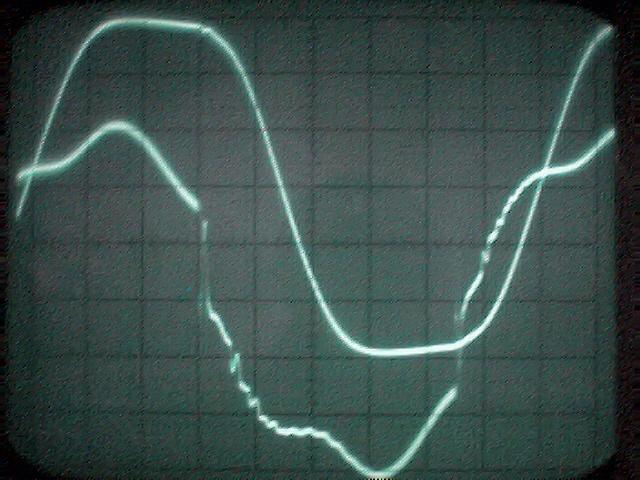
Ici j’ai affiché courant et tension
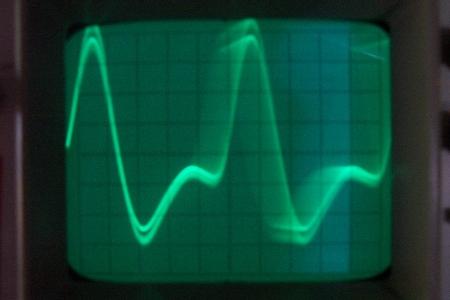
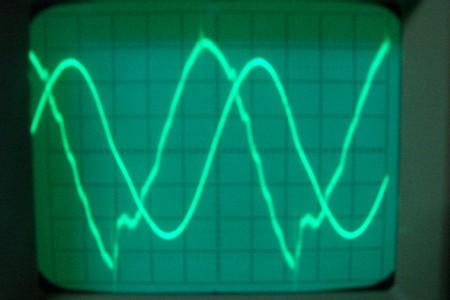
La puissance sera inférieure à celle du même signal sinusoïdal variant de U=-600V à +800V. C’est une très grosse approximation, mais même ainsi on trouve une puissance de
Puissance de sortie = Pout= U²/(2xR) = 700²/(2×120 000) = 2 Watts
Et en réalité on est bien au-dessous de cette valeur. Même alors cela donne: COP = 0.5
COP < 0,5
3) Conclusion
Le générateur de fréquence qui a permis de faire varier la forme des signaux d’entrée ainsi que la fréquence au-delà de celle permise par le contrôleur n’a rien apporté de plus au MEG qui ne marche toujours pas.
Le MEG : Théorie selon son auteur
A peu d’intérêt au vu du fait que l’expérience ne fonctionne pas, mais je donne à titre indicatif
1/ Lien entre MEG et électrodynamique
Cette invention se base sur les propriétés dynamiques des champs magnétiques manifestées par certains matériaux notamment utilisés pour la fabrication du noyau des transformateurs électriques. L’analyse, dans le cadre de l’électrodynamique O(3), de l’équilibre dynamique de l’énergie volumique du champ magnétique généré par un matériau à aimantation permanente, autorise un « pompage » d’énergie du vide par l’intermédiaire d’une reconstitution « asymétrique » de l’énergie volumique (potentiel scalaire) à partir des courants du vide. C’est ici qu’interviennent les fameuses densités de courants du vide décrites dans les équations de Lehnert. L’originalité du procédé consiste à créer et à entretenir un phénomène transitoire de régénération de cette énergie volumique. L’énergie magnétique récoltée à chaque phase est directement transformée en courant électrique alternatif, comme dans un banal transformateur. Les fréquences utilisées sont les fréquences habituelles (de l’ordre des dizaines de Hertz). L’ensemble du procédé sera entièrement décrit dans le texte qui accompagnera le brevet qui devrait être prochainement délivré par l’administration américaine après une âpre bataille avec les inventeurs. Performances: l’appareil affiche un coefficient de performance nettement supérieur à l’unité, c’est à dire que l’énergie récoltée par le fonctionnement de la machine est nettement supérieure à celle qui est nécessaire à l’entretien de son fonctionnement. Le français Jean-Louis Naudin est l’un des premiers à avoir répliqué avec succès cette technologie. Les inventeurs sont au nombre de quatre, parmi lesquels figure T. Bearden, et la commercialisation de cette technologie est gérée par la société Magnetic Energy Limited .
Voir « Derivation of the Lehnert field equations from gauge theory in vacuum: Space charge and current » Foundations Of Physics Letters, 13(2), avr 2000, pp.179-184.
D’après: http://(…)ElectroDyn_FR.rtf
Il existe plusieurs théories d’électrodynamique, 3 majeures:
Électrodynamique de Maxwell-Heaviside: Courants du vide: inexistants et impossibles; les incohérences sont inhérentes, dans le fameux courant de déplacement de Maxwell, au fait qu’il n’y a pas de densité de charge d’espace correspondante dans le vide. Il est montré que si la condition de Lorentz n’est pas prise en considération, les équations de champ de Maxwell-Heaviside deviennent les équations de Lehnert, qui indiquent la présence d’une densité de charge et d’une densité de courant dans le vide.
Électrodynamique Quantique: Courants du vide: modifications et influences locales des potentiels scalaires du vide (polarisations virtuelles à l’échelle des particules, effet Aharonov-Bohm)
Électrodynamique O(3) développée par M.W.Evans à partir des travaux de Mendel Sachs: Courants du vide possibles: les équations de champ de Lehnert dans le vide (qui sont un sous-ensemble des équations de champ O(3) de Yang-Mills), avec leurs densités de courants et leurs densités de charges du vide correspondantes, peuvent être dérivées directement de la théorie de jauge standard appliquée au vide, en utilisant le concept de dérivée covariante et celle d’influence universelle de Feynman.
D’après: http://(…)U(1)vsO(3).htm
2/ Équations de champ de Lehnert et utilisation en électrodynamique
Résumé de la théorie de Lehnert : Il est montré que les équations de champ de Lehnert dans le vide, avec leur densité spatiale de courant et de charge, peuvent être dérivées directement de la théorie standard des champs de jauge appliquée au vide, en utilisant les concepts de dérivée covariante et de perturbation universelle de Feynman. Il est montré une interrelation entre les équations de champ de Lehnert et celles de Proca à travers le célèbre théorème de de Broglie, dans lequel la masse du photon peut être interprétée comme finie. Ces idées vont dans le sens de la mise en cause d’une incohérence dans le fameux courant de déplacement de Maxwell, qui n’a pas de densité de charge de vide correspondante. D’après: NII-REO
Hypothèses de travail et réflexions de Lehnert:
Les équations de Maxwell ont été modifiées sur la base de deux hypothèses:
1. La divergence du champ électrique peut différer de zéro dans le vide.
2. Les équations de champ doivent rester invariantes par transformation de Lorentz.
Les équations de Maxwell dans le vide ont été modifiées en affectant un coefficient de conductivité au vide petit mais non nul (sigma différent de 0). Ceci donne lieu à un déplacement de courant comme déjà observé par Bartlet et al. Si nous assignons un coefficient de conductivité non nul au vide de Maxwell au lieu d’une charge spatiale, alors le photon perd son énergie quand il se propage à travers un tel vide. Mais pour rendre cette étude pleinement relativiste, il est nécessaire d’introduireune une charge spatiale dans le vide.
Conclusions de l’étude:
L’isotropie et l’homogénéité de notre univers sont les deux composants de base du principe cosmologique. 1. L’hypothèse d’une masse restante non nulle pour le photon conduit à la violation d’isotropie des propriétés de la lumière.
2. Plusieurs tentatives ont été faites pour relier la masse restante non nulle du photon avec le procédé de dissipation du vide qui amène à une interprétation du décalage vers le rouge (redshift) des lignes spectrales à l’échelle cosmologique.
3. Les évènements astrophysiques récents à fort décalage vers le rouge peuvent être utilisés pour imposer des limites strictes aux variations de la vitesse de la lumière, la masse du photon et l’échelle d’énergie de la gravité quantique.
D’après:http://(…)V07N1LEH.pdf
3/ Fonctionnement électrodynamique du MEG
3.1. Fondements théoriques
Il n’y a aucun substitut en science à la lecture de cette littérature. Ce n’est pas à moi de convaincre d’autres expérimentateurs de quoi que ce soit; ils peuvent « croire » ce qu’ils veulent. Ce n’est pas une matière de « croyance » de toute manière, mais une matière de ce que nous avons fait et ce que nous utilisons, et de ce que la physique a à dire à ce propos. Si quelqu’un ne comprend pas la différence entre un potentiel vectoriel magnétique sans courbure A, et un potentiel vectoriel magnétique courbé A, alors il ne comprendra jamais le MEG et son fonctionnement. Si quelqu’un est intéressé sérieusement et par ses aspects techniques à savoir comment l’énergie est extraite du vide local par le MEG, il y a deux documents d’électrodynamique plus ardue de symétrie de groupe sur le MEG qui ont été publiés par l’AIAS dans « Foundations of Physics Letters ». Ces documents très techniques expliquent le processus par lequel l’énergie est extraite du vide. Par : Thomas E. Bearden, Co-inventeur du MEG. D’après: http://(…)energy.htm
3.1.1. Explication du MEG avec l’électrodynamique O(3) :
Résumé : Récemment, Bearden et associés ont développés un dispositif connu sous le nom de générateur électromagnétique sans mouvement (MEG) qui produit un coefficient de performance (COP) largement excédentaire à l’unité. Ce dispositif a été reproduit indépendamment par Naudin. Dans ce document, le principe opérationnel fondamental du MEG est expliqué en utilisant une version hautement symétrique de l’électrodynamique connue sous le nom d’électrdynamique O(3), qui est basée sur l’existence empirique de deux états de polarisation circulaires de la radiation électromagnétique, et qui a été développé de manière intensive dans la littérature. L’explication théorique du MEG avec l’électrodynamique O(3) est simple: l’énergie magnétique est extraite directement du vide et utilisée pour remplir les aimants permanents du dispositif MEG, qui produit alors une source d’énergie qui, en théorie, peut être renouvelée indéfiniment à partir du vide. Un tel résultat est incompréhensible en électrodynamique U (1) de Maxwell-Heaviside. D’après: http://(…)4&I=6.
Explanation of the Motionless Electromagnetic Generator with O(3) Electrodynamics)
Foundations of Physics Letters Vol. 14., No. 1: 87-94; Feb 2001
par: P. K. Anastasovski, T. E. Bearden, C. Ciubotariu, W. T. Coffey, L. B. Crowell, G. J. Evans, M. W. Evans, R. Flower, A. Labounsky, B. Lehnert, M. Mészáros, P. R. Molnár, J. K. Moscicki, S. Roy, J. P. Vigier. Article ici: http://www.cheniere.org(…)index.php
3.1.2. Explication du MEG avec la théorie électrodynamique de Sachs :
Résumé : Il est démontré que les principes de relativité générale développés par Sachs peuvent être utilisés pour expliquer le sprincipes du générateur électromagnétique sans mouvement (MEG), qui extraits l’énergie électromagnétique de l’espace-temps courbe de Rieman et en conséquence produit approximativement 20 fois plus d’énergie que consommé. Donc, il est montré de manière la plus générale que l’énergie électromagnétique pzut être extraite à partir du vide et utilisée pour alimenter des dispositifs opérationnels comme le MEG, dispositifs qui sont reproductibles et répétables.
Explanation of the Motionless Electromagnetic Generator by Sachs’s Theory of Electrodynamics
Foundations of Physics Letters Vol. 14., No. 4: 387-393; Aug 2001
par: P. K. Anastasovski, T. E. Bearden, C. Ciubotariu, W. T. Coffey, L. B. Crowell, G. J. Evans, M. W. Evans, R. Flower, A. Labounsky, B. Lehnert, M. Mészáros, P. R. Molnár, J. K. Moscicki, S. Roy, J. P. Vigier. Article ici: http://www.cheniere.org/references/megsachs/index.htm
3.1.3. Liens entre les deux théories :
3.2. Fonctionnement technique détaillé du MEG, liens.
http://web.archive.org/web/20051024082640/http://www.help4all.de/energy/MEGpaper.pdf
Brevet: http://www.cheniere.org/references/MEG_Patent.pdf
Le MEG : LIENS
The Motionless Electromagnetic Generator (MEG) / The Tom Bearden Website
http://www.cheniere.org/megstatus.htm
Motionless Electromagnetic Generator (MEG) / rexresearch.com
http://www.rexresearch.com/meg/meg.htm
The Motionless Electromagnetic Generator / JLN Labs home page
http://jnaudin.free.fr/meg/meg.htm
Scalar Wars / Scalar Electromagnetics